Meta-Control: Automatic Model-based
Control System Synthesis for Heterogeneous Robot Skills

Tianhao Wei*,1, Liqian Ma*,1,2, Rui Chen1, Weiye Zhao1, Changliu Liu1,
*Equal Contribution, 1Carnegie Mellon University, 2Tsinghua University
Paper Video Code (Coming soon)

All videos are in real time.

Abstract

The requirements for real-world manipulation tasks are diverse and often conflicting; some tasks require precise motion while others require force compliance; some tasks require avoidance of certain regions while others require convergence to certain states. Satisfying these varied requirements with a fixed state-action representation and control strategy is challenging, impeding the development of a universal robotic foundation model. In this work, we propose Meta-Control, the first LLM-enabled automatic control synthesis approach that creates customized state representations and control strategies tailored to specific tasks. Our core insight is that a meta-control system can be built to automate the thought process that human experts use to design control systems. Specifically, human experts heavily use a model-based, hierarchical (from abstract to concrete) thought model, then compose various dynamic models and controllers together to form a control system. Meta-Control mimics the thought model and harness LLM's extensive control knowledge with Socrates' "art of midwifery" to automate the thought process. Meta-Control stands out for its fully model-based nature, allowing rigorous analysis, generalizability, robustness, efficient parameter tuning, and reliable real-time execution.



Heterogeneous Robot Skills

Real-world manipulation tasks have inherently different and even opposite requirements. Using an inapproriate representation or control strategy may lead to failure or dangerous behaviors during manipulation. Therefore, a method to customize representation and control strategy is needed.

Failure: Wipe the whiteboard with a Cartesian trajectory planner. Failed because force constraints can not be specified.

Failure: Open the cabinet with a joint space planner. Failed because planned swing path is not accurate.

Failure: Balance a cart pole with a MPC. Failed because the feedback frequency is too low.

To address this problem, Meta-Control finds the most approriate representations and control strategies on the fly for heterogeneous robot skills.

Meta-Control: Gripepr planner + force pose hybrid controller. Maintain contact force on the whiteboard.

Meta-Control: Cartesian space planner + stiffness controller. Executable even with inaccurate swing path.

Meta-Control: High frequency LQR for the cart + hybrid pose force tracking.

Meta-Control Method



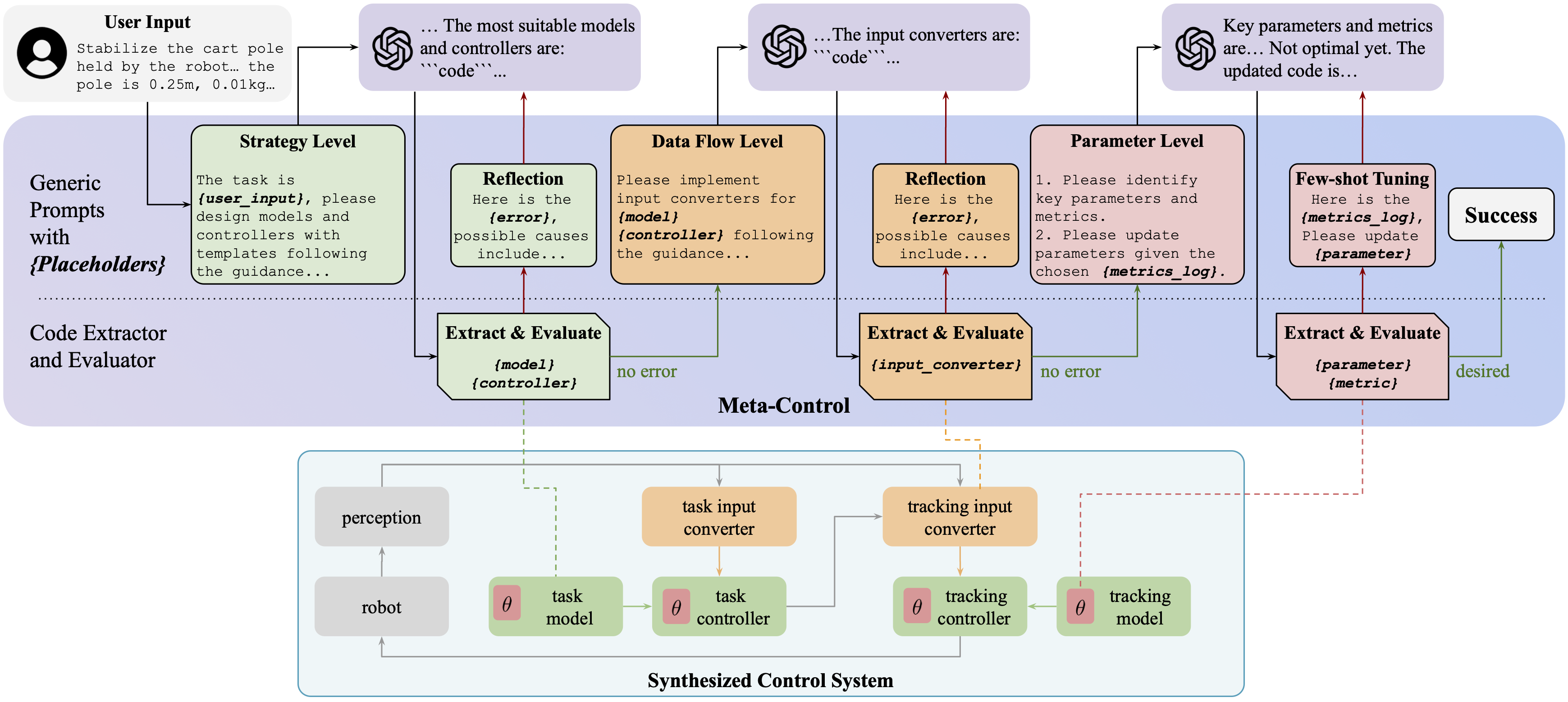
Overview of Meta-Control: The user only needs to provide a skill description. Meta-Control then leverages the control knowledge of LLMs to synthesize skills through a three-level pipeline: strategy level, data flow level, and parameter level. For each level, we have designed a generic prompt with placeholders, which are dynamically replaced with user input or code extracted from the LLM response during runtime, utilizing a code extractor to make the prompt task-specific. The extracted code is also used to construct the control system. At each level, if the LLM-generated code results in an error, a reflection phase is initiated. We have embedded design principles and checklists of common errors within the design and reflection prompts to assist the LLM in producing correct code. The generic prompt design with placeholders allows Meta-Control to generalize to unseen tasks without modification.


Satisfying Diverse Task Requirements

Meta-Control can satisfy diverse task requirements that may happen in open world manipulation tasks, such as

  • High Frequency Closed-loop Control: Meta-Control designs a LQR controller with a linearized dynamic model to compute the desired force on the cart, and designs a hybrid pose force controller to track the desired force and the neutral position at the same time. This design enables high-frequency closed-loop control, and guarantees convergence.
  • Compliant Execution: Meta-Control designs a Cartesian space planner to decide the desired goal position of the door knob, then use a impedance controller to track the desired position while remaining compliant to external forces that caused by trajectory mismatch with the swing path, leading to a smooth and safe execution.
  • Collison Avoidance: Meta-Control first use a MPC controller to plan collison free waypoints for the gripper, then track the way points with a safe controller, which can guarantee collision avoidance for the whole arm.


    • Generalization to Different Embodiments

    Meta-Control synthesized control system is fully model-based, enabling generalization to different embodiments. For instance, a control system synthesized on Kinova Gen3 can easily directly generalize to a Franka Panda robot.


    Generalization to Different Scenarios

    Meta-Control synthesized control system can easily generalize to scenarios of different states thanks to the model-based nature.

    initial pole angle = +0.1 rad

    door width = 0.3 m

    object arrangement 1



    initial pole angle = -0.5 rad

    door width = 0.6 m

    object arrangement 2

    Exploiting Dynamical Priors Internalized by LLM

    For tasks involving unknown dynamics, Meta-Control can exploit dynamics prior internalized by LLM. For example, in the balance cart pole task. The dynamics of the whole system is unknown. But Meta-Control can give an analytical approximation of the system on the task level. The synthesized control system for this task is shown below. For simplicity, we describe them by text. Specifically, the task level system is modeled as the linearized dynamics in the form of $\dot z = A z + B v$ around the upright position of the pole, where $A$ and $B$ are directly given by the LLM. Exploiting dynamics priors enables Meta-Control to synthesize high-performance controllers rigorously.

    Task level \begin{align} \text{State} &= [\text{Pole}_\theta, \text{Pole}_{\omega}, \text{Cart}_y, \text{Cart}_{\dot y}]\\ \text{Control} &= \text{Desired force on the cart}\\ \text{Dynamics} &= \text{Linear Dynamic Model}\\ \text{Controller} &= \text{LQR controller} \end{align}
    Tracking level \begin{align} \text{State} & = \text{Joint states}, \text{EE}^{\text{target}}_{\text{force}}, \text{EE}^{\text{target}}_{\text{pose}}\\ \text{Control} &= \text{Joint torques}\\ \text{Dynamics} &= \text{Kinova Dynamic Model}\\ \text{Controller} &= \text{Pose Force Controller} \end{align}
    Analytical task level dynamic model: \begin{align} \dot z &= \begin{pmatrix} 0 & 1 & 0 & 0 \\ 0 & 0 & \frac{m_{\text{pole}}g}{m_{\text{cart}}} & 0 \\ 0 & 0 & 0 & 1 \\ 0 & 0 & \frac{g(m_{\text{cart}}+m_{\text{pole}})}{l_{\text{pole}}m_{\text{cart}}} & 0 \end{pmatrix} z + \begin{pmatrix} 0 \\ \frac{1}{m_{\text{cart}}} \\ 0 \\ -\frac{1}{l_{\text{pole}}m_{\text{cart}}} \end{pmatrix} v. \end{align}

    Efficient System Parameters Tuning

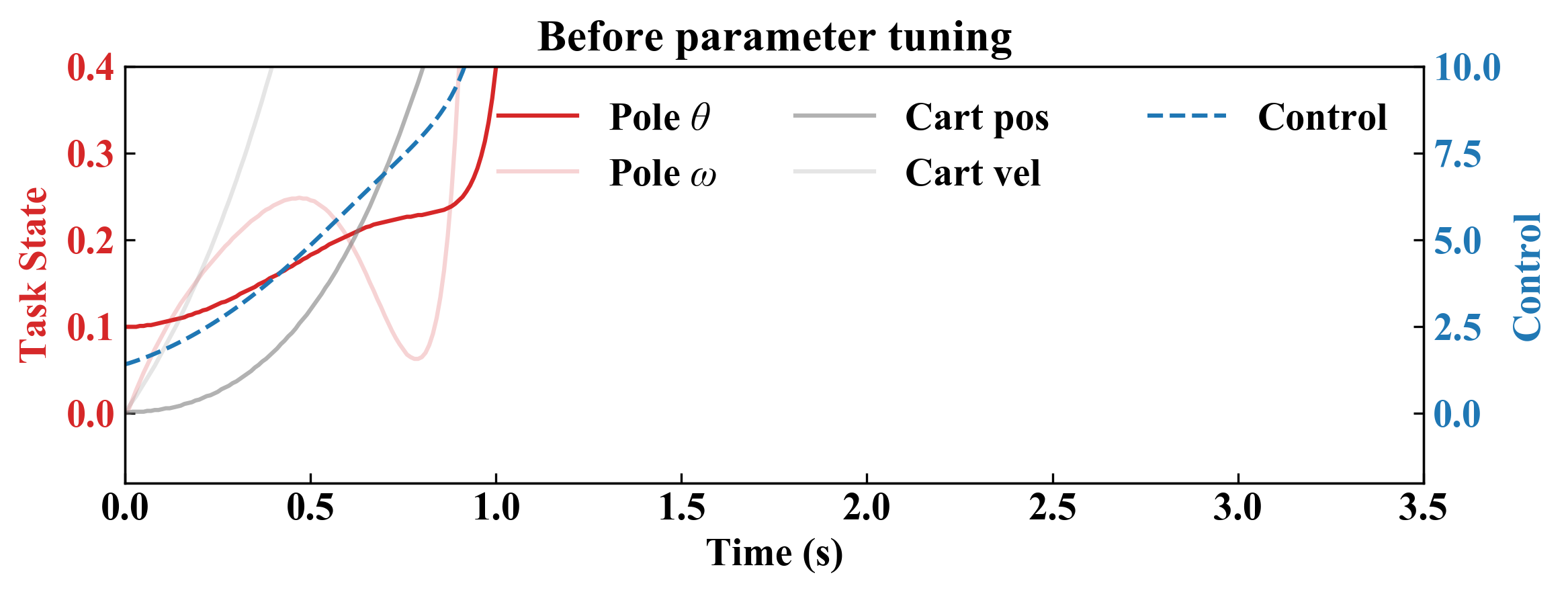
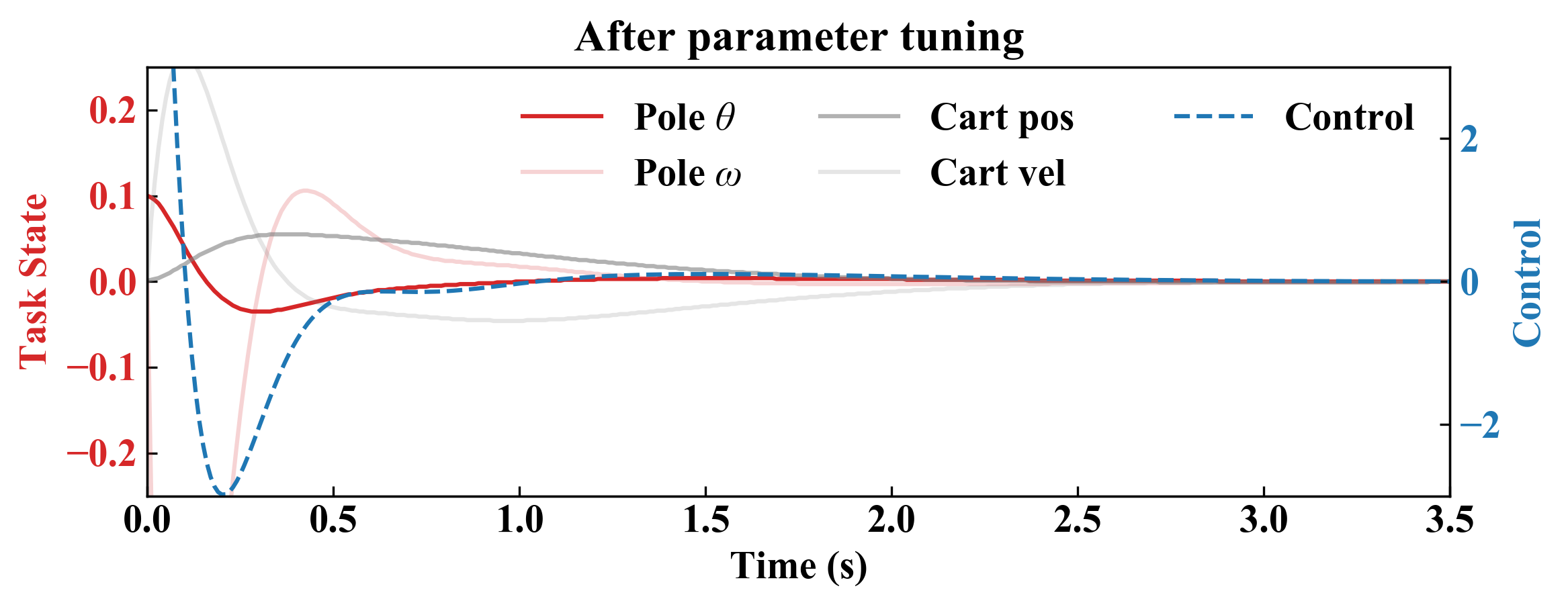
    Meta-Control can efficiently tune the parameters of the chosen models and controllers to achieve the desired performance. For example, Meta-Control chooses an LQR controller for the balance task, where the Q and R matrices are critical to the performance. Before parameter tuning, the model fails to balance the pole. But with only two rounds of execution, Meta-Control finds the proper parameter that successfully balance the pole.

    Rigorous Formal Analysis

    Meta-Control synthesized controller is fully model-based. Therefore, we can give rigourous analysis and guarantees for the synthesized control system.

  • Forward Invariance: In the safe pick&place task, the chosen tracking controller involves a safety index (control barrier function), which can guarantee collision avoidance by keeping the robot state stay in the safe set. Formally, let $d_{\text{min}}$ be the allowable minimum distance, $d(x)$ and $\dot d(x)$ be the relative distance and relative velocity from the robot to the obstacle, respectively. Then the following inequality always holds: $$\min\{d_{\text{min}}-d(x), 100\cdot(0.02^2 - d(x)^2) - 10 \cdot \dot d(x)\} < 0$$
  • Stability and Convergence: For the balance cart-pole task, we can provide a convergence guarantee by solving the Riccati equation for the LQR task controller. The close-loop system matrix $A - BK$ has the following four eigenvalues: $$-412.29, -9.925, -1.502+1.175j, -1.502-1.175j.$$ All of them have negative real parts. Therefore, the system is guaranteed to converge. More advanced analysis can be applied to take the linearization error into consideration and provide more rigorous guarantees.

    • Prompts

    Prompts of the Composer:
    Design Composer | Implementation Composer | Parameter Tuning Composer

    Prompts of the control system synthesis:
    Design Models and Controllers | Design Reflection | Design Summary | Task Controller Implementation | Tracking Controller Implementation | Implementation Reflection | Parameter Tuning | Dynamic Model Templates | Controller Templates | Input Port Samples

    Prompts of the tasks:
    Reach the Goal with Collision Avoidance | Wipe the Whiteboard | Open the Door | Balance the Cart Pole |